JAVASCRIPT EXECUTION LIMITS IN THE WEB BROWSER
When we ask the visualization of a web page in the browser, it could shows you:
Warning: Unresponsive script" prompt that says "A script on this page may be busy, or it may have stopped responding. You can stop the script now, or you can continue to see if the script will complete."
It means that a script takes too long to run and the browser doesn’t accept it.
A consequence of it is that the user interaction with the browser and web page is stopped.
The browser UI and JavaScript code share a single processing thread. Every event is added to a single queue. When the browser becomes idle, it retrieves the next event on the queue and executes it.
In reality, browsers starts a new OS process for every tab. However, there is still a single event queue per viewed page and only one task can be completed at a time. This is necessary for rendering the web page and for the user interaction with the web page in the browser.
To test the speed and limit of web browser in the execution of the JavaScript code we are going to use a heavy processing algorithm for generation of combinations without repetitions.
DONALD KNUTH’S ALGORITHM FOR GENERATION OF COMBINATIONS WITHOUT REPETITIONS
The number of combinations of n things, taken k at a time are exactly:
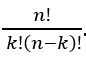
We can think these n things as an ordered collection of objects and we can use binary notation to discover combinations.
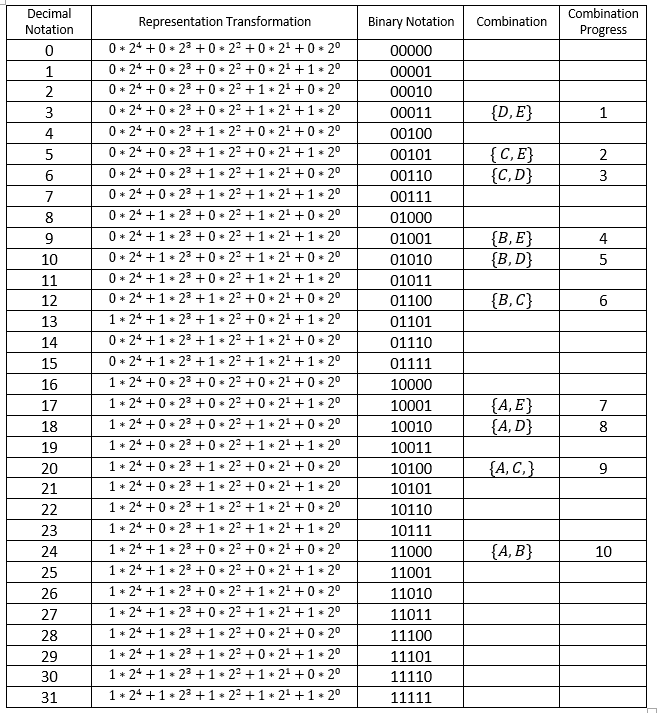
For example, we take a set of five letter: {A,B,C,D,E} and we want to list the combinations of 2 letter from this set without repetitions. Using the formula above the number of combinations is 10.
We consider this set as an ordered set: A<B<C<D<E and we use the binary notation to represent it where
0 means the letter is not in the combination and 1 means the letter is in the combination.
We know that the number of all subsets is = 32 > 5, while we have to select of these subsets only those that have a number of elements equal to 2.
Considering the set as an ordered set {A,B,C,D,E} and using the binary notation, the list of all subsets of this set are:
Only good binary representations are used to generate good combinations.
Here it is a combination tool.
A program in JavaScript to codify the algorithm could be:
//--------------------------------------------------------------------
function GenerateCombinations()
{
var Answer_Head = "<table border='1' >";
var Answer_Body = "";
var Answer_Tail = "</table>";
var ErrorCode = 0;
var ErrorMsg = "";
var nCombSize = 0;
var BaseComb = new Array();
var iBaseComb = 0;
var CodeComb = 0;
var CombList = new Array();
var ACombItem = "";
var BinaryNumber = new Array();
var BinaryStringNumber = "";
var NProgres = 0;
var RNProgres = 0;
var NFilter = 0;
var Start = Date.now();
var End = Date.now();
var Elapsed = End - Start // time in ms
var cElapsed = Elapsed.toString();
// AREA INTELLIGENCE
// Clear Area
window.document.getElementById("i_BackMsg").innerHTML = "" ;
window.document.getElementById("i_Answer").innerHTML = ""
// Check Input Data
if ( isNaN( window.document.getElementById("iN").value) ) {
ErrorCode = 1;
ErroMsg = "Attention !!! The Combination Size must be a number.";
}
else {
if (window.document.getElementById("iN").value == 0 ||
window.document.getElementById("iN").value == "" ) {
ErrorCode = 11;
ErroMsg = "Attention !!! The Combination Size must be a value more then zero.";
}
else
{
if (window.document.getElementById("iN").value >= 20 ) {
ErrorCode = 11;
ErroMsg = "Attention !!! The Combination Size must less then 20.";
}
else
{
nCombSize = window.document.getElementById("iN").value ;
};
};
};
// Show Msg
if ( ErrorCode > 0 ) { window.document.getElementById("i_BackMsg").innerHTML =ErroMsg+"<br/>" ;
return;
}
else
{
window.document.getElementById("i_BackMsg").innerHTML ="OK!" ;
};
// Check Elements
iBaseComb = 0;
if ( !(window.document.getElementById("i_e01").value == "" ||
window.document.getElementById("i_e01").value == "0" )) {
BaseComb[iBaseComb]=window.document.getElementById("i_e01").value;
iBaseComb++;
};
< .... >
if ( !(window.document.getElementById("i_e20").value == "" ||
window.document.getElementById("i_e20").value == "0" )) {
BaseComb[iBaseComb]=window.document.getElementById("i_e20").value;
iBaseComb++;
};
if ( iBaseComb == 0 || iBaseComb <= nCombSize ) {
ErrorCode = 11;
ErroMsg = "Attention !!! The Elements must not be equal to or more than the combination size.";
};
// Show Msg
if ( ErrorCode > 0 ) {
window.document.getElementById("i_BackMsg").innerHTML =ErroMsg+"<br/>" ;
return;
}
else
{
window.document.getElementById("i_BackMsg").innerHTML = "" ;
};
// Combination Code
CodeComb=0;
for (j=0;j<=iBaseComb-1;j++){
CodeComb+= Math.pow(2,j);
};
// Combination Generator
CombList = new Array(iBaseComb);
for (y=0;y<=CombList.length-1;y++){
CombList[y]="0"
};
RNProgress = 0;
NProgres = 0;
for (k=0;k<=(CodeComb); k++) {
BinaryNumber = DecimalToBinary(k, iBaseComb);
if ( IsAGoodCombination (BinaryNumber, nCombSize ) ) {
for (y=0;y<=CombList.length-1;y++){
CombList[y]="0";
};
// Make the combination
for (x=0;x<=BinaryNumber.length-1;x++){
if (BinaryNumber[x]=="1"){
CombList[x]=BaseComb[x];
};
};
CombList.sort(function(a,b){return a - b});
NProgres++;
ACombItem="";
for (j=0;j<CombList.length;j++){
if (CombList[j]!="0"){
ACombItem=ACombItem+CombList[j]+" ";
};
};
window.document.getElementById("i_Answer").innerHTML+=NProgres.toString()+" - ";
window.document.getElementById("i_Answer").innerHTML+=ACombItem+"<br />";
};
};
window.document.getElementById("i_Answer").innerHTML+=Answer_Tail+"<br /><br />";
End = Date.now();
Elapsed = End - Start // time in milliseconds
cElapsed = Elapsed.toString();
window.document.getElementById("i_Time").innerHTML="Time Elapsed: "+cElapsed+" ms";
return ;
}
//--------------------------------------------------------------------
function DecimalToBinary (iDecNumber, iSize){
// Section Data Structure
answer = new Array(iSize);
n10 = iDecNumber;
x2 = iDecNumber;
log2 = 0;
// Section Initialization
for (j=0; j<=answer.length-1;j++){
answer[j]="0";
};
// Section Intelligence
while (x2>=2) {
x2=x2/2;
log2++;
};
for (l2=log2;l2>=0;l2--) {
power = Math.pow(2,l2);
if (n10 >= power) {
answer[l2]="1";
n10 = n10 - power;
}
else {
answer[l2]="0";
};
};
answer.reverse();
return answer
}
//--------------------------------------------------------------------
function IsAGoodCombination ( iBRNumber, iCombSize ) {
var NumberOfOne = 0 ;
for (j=0;j<=iBRNumber.length-1;j++) {
if (iBRNumber[j]=="1") {
NumberOfOne++;
if ( NumberOfOne > iCombSize ) {
break;
};
};
};
if ( NumberOfOne == iCombSize ) {
return true;
}
else {
return false;
};
}
//--------------------------------------------------------------------WEB APPLICATION CLIENT-SIDE JAVASCRIPT PERFORMANCE
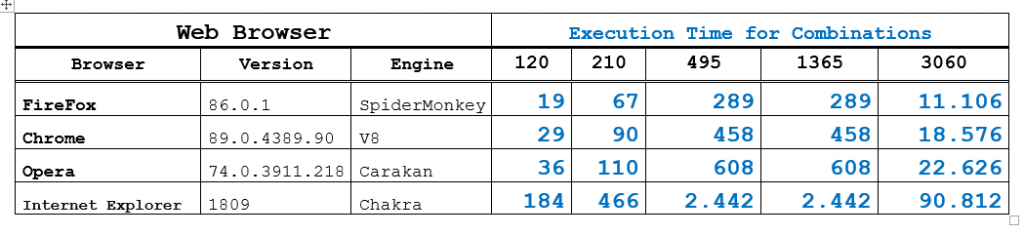
The results of using as benchmark the JavaScript program previously described are the following ones.
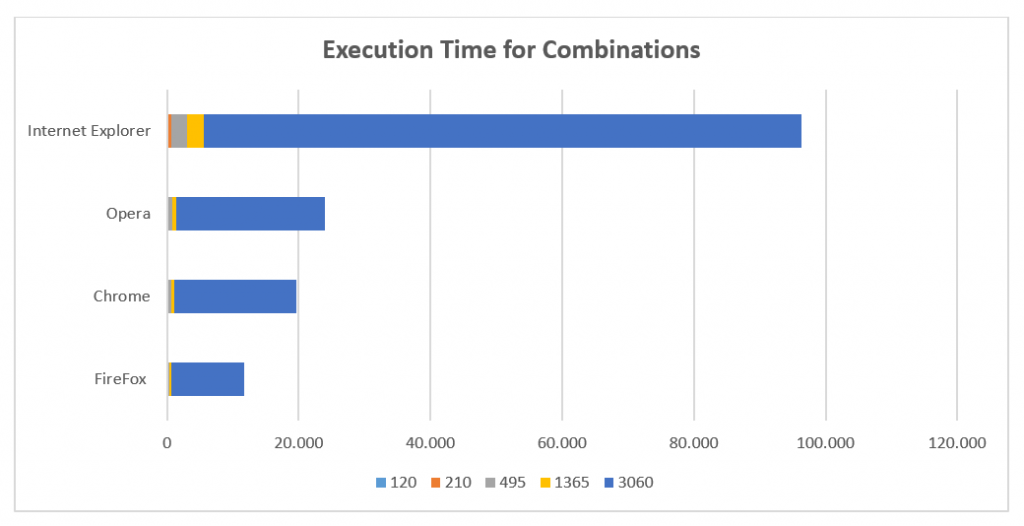
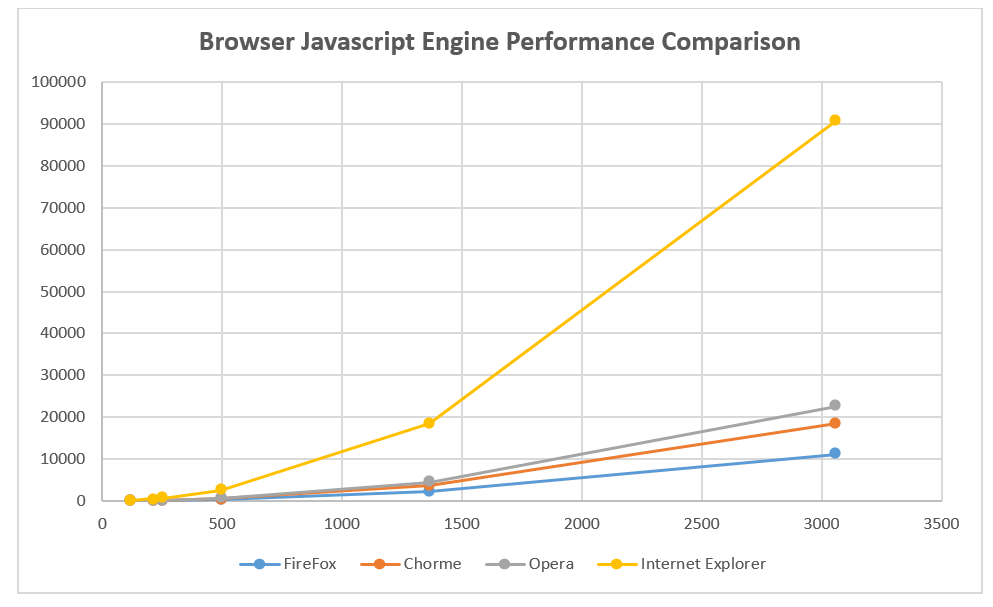
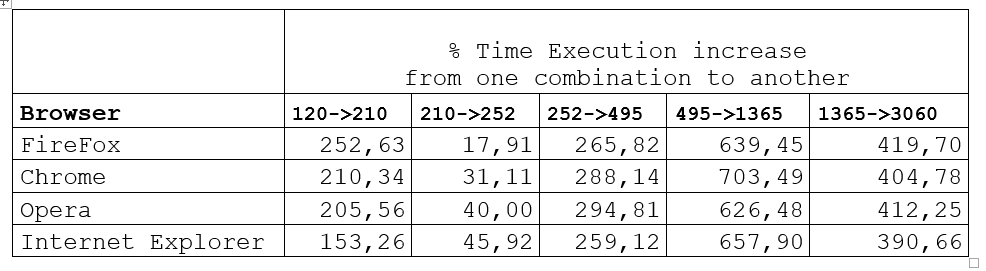
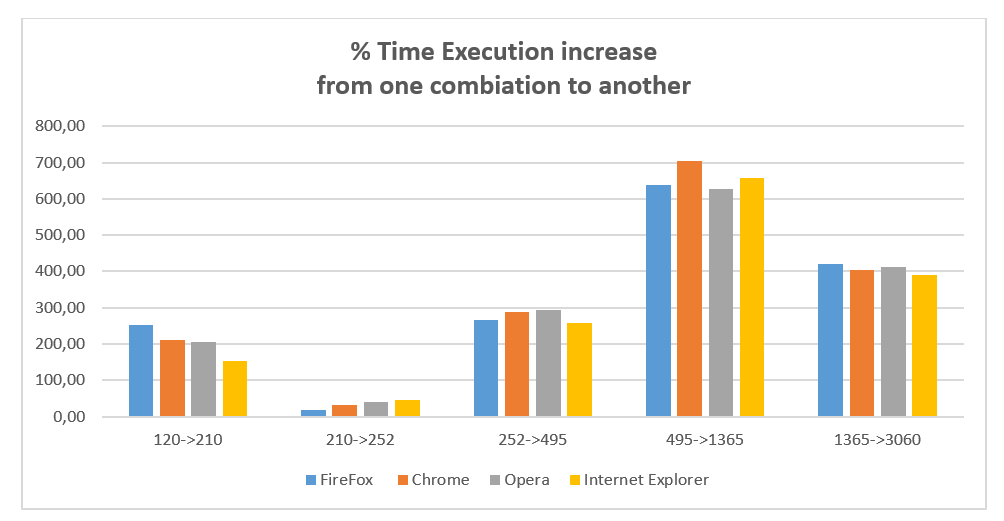
How we can see from the tables and graphs above SpiderMonkey Engine in this test result the winner.
Only in the increase of execution time for high number of combinations it is not the best.
REFERENCES
[01] Donald E. Knuth, The Art of Computer Programming Volume 4 Generating All Combinations and Partitions Fascicle 3, July 2005;
[02] JavaScript Execution and Browser Limits https://www.sitepoint.com/javascript-execution-browser-limits/ ;
[03] Web Browser http://www.volucer.it/?p=143